Aviso: O conteúdo aqui apresentado tem uma finalidade exclusivamente informativa sobre um tipo específico de jogo e como jogá-lo. O objetivo deste conteúdo não é nem promover nem disponibilizar um tipo de jogo, mas simplesmente informar o jogador acerca de como jogá-lo.
O poker é um jogo carregado de matemática e com base em estatística. Apesar da vitória não estar sempre garantida, implementar uma estratégia no nosso jogo que seja propícia a seguir probabilidades do poker corretas e pot odds aumentará, sem dúvida, as suas probabilidades de sucesso nas mesas.
A estratégia envolve uma parte do jogo que lida com o cálculo de (1) outs (que ajudam a definir as percentagens no poker), (2) pot odds (pot odds) e (3) a sua equidade no pote. Apesar dos três conceitos andarem de mãos dadas, o nosso foco principal neste artigo será explorar os dois primeiros.
Vamos discutir aquilo que são as odds no poker e as probabilidades associadas ao jogo para o ajudar a compreender a probabilidade de eventos em específico e para o ensinar, também, a implementar uma boa estratégia geral no seu jogo de poker com probabilidades em mente.
E para facilitar, pode sempre usar a calculadora de odds da 888poker:
Índice
- Probabilidade das Mãos de Poker
- Probabilidades de Receber Determinadas Hole Cards no Poker
- Probabilidades de Completar uma Mão no Flop
- Melhorar os Seus Draws
- O Que São Pot Odds no Poker?
- Como Ler as Pot Odds em Percentagens, Frações e Rácios
- Fórmula de Pot Odds no Poker
- Como Funcionam as Pot Odds
- Regras Básicas de Probabilidades no Poker
- Como Converter Pot Odds em Percentagens
- Quando Fazer Call Utilizando Pot Odds
- Como Calcular Pot Odds em Texas Hold'em
- Como Calcular Pot Odds em Omaha
- Calcular Probabilidades no Poker Heads-Up
- Sumário: Porquê Calcular Pot Odds
Probabilidade das Mãos de Poker
Há 2.598.960 mãos de 5 cartas distintas que podem ser feitas no poker. Olhemos para a forma como estas combinações se dividem entre os vários tipos de mãos que se podem completar nesta tabela de probabilidades do poker:
| Mão de Poker | Frequência (Mãos Distintas) | Probabilidade (%) | Odds (~) |
|---|---|---|---|
| Royal Flush | 4 | 0.000154% | 1 em 649,740 |
| Straight Flush | 36 | 0.00139% | 1 em 72,193 |
| Quads/Poker | 624 | 0.0240% | 1 em 4,165 |
| Full House | 3,744 | 0.1441% | 1 em 694 |
| Flush | 5,108 | 0.1965% | 1 em 509 |
| Straight | 10,200 | 0.3925% | 1 em 255 |
| Trio | 54,912 | 2.1128% | 1 em 47 |
| Dois Pares | 123,552 | 4.7539% | 1 em 21 |
| Um Par | 1,098,240 | 42.2569% | 1 em 2.4 |
| Carta Alta | 1,302,540 | 50.1177% | 1 em 2 |
Há algumas coisas a salientar em relação a esta tabela de probabilidades:
- O ranking de mãos sobe sequencialmente da mão mais fácil para a mais difícil (menos provável) de ter. (Por isso, você agora sabe porque é que os flushes são melhores do que straights/sequências em Texas Hold'em.)
- A probabilidade de um par no poker é ~42%.
- As probabilidades de completar um full house no poker são menores do que 1% (~0.1441%).
- A probabilidade de completar um Royal Flush em Texas Hold'em é de apenas 1 a cada 649.740 mãos!
- A probabilidade de completar um straight flush no poker é de 1 a cada 72.193 mãos ou 0.00139%.
Por favor, consulte esta tabela para determinar qual a probabilidade de completar uma mão de poker em específico.
Probabilidades de Receber Determinadas Hole Cards no Poker
Multiplique 52 cartas num baralho de poker normal por 51 (para segunda carta) e depois divida esse resultado por 2 (porque receber A♣K♠ é a mesma coisa que receber K♠A♣, por exemplo - apenas a ordem é diferente). Você verá que há 1.326 combinações únicas de 2 cartas que poderá receber em Texas Hold'em.

Aprofundando esta questão, se recebe uma mão como AK, pode multiplicar os 4 Ases pelos 4 Reis e ver que há 16 combinações de AK no total, tanto suited como off-suit.
Destes 16 combos, considerando que há 4 naipes num baralho de poker, 4 destas combinações de AK serão suited, deixando 12 combinações não-suited de mãos sem pares (os mesmos valores aplicam-se a qualquer mão de poker que não sejam pares de mão). Para pares de mão, haverá 6 combinações de cada.
Conhecendo a informação acima, poderemos depois fazer cálculos básicos para determinar a probabilidade de receber certas combinações de hole cards.
Por exemplo, para par de Ases, dividiríamos 6 combos por 1.326 combinações totais para ver que receberemos esta mão 1 vez a cada 221 mãos, em média.
Para qualquer mão suited específica, por haver apenas 4 combos de cada (em vez de 6 como com os pares de mão), você receberá mãos suited sem par (de valores específicos) menos frequentemente do que receberá pares de mão. Posto isto, receberá uma mão como AKs especificamente 1 vez a cada 332 mãos, em média. O que significa que receberá Ases mais frequentemente do que AKs.
Para o último ponto deste capítulo, caso queira saber quais as probabilidades de receber mão X ou melhor, adicione simplesmente o número de combinações para cada mão.
Por exemplo, se quisermos saber quais a probabilidades de receber QQ+ e/ou AK, veremos que há 18 combos de pares de mão e 16 combos de AK, totalizando 34 combos.
Dividindo 1.326 combos totais por 34 destes combos específicos, concluímos que receberemos AK ou QQ+ cerca de 1 vez a cada 39 mãos.
Segue uma tabela que sumariza a informação essencial sobre hole cards que delineámos acima e que dá informação extra sobre a probabilidade de receber combinações específicas:
| Mão | Combinações Totais de Mãos | Probabilidade (%) | Odds |
|---|---|---|---|
| Quaisquer duas cartas | 1326 | 100% | 1 em 1 |
| AK (qualquer mão específica) | 16 | 1.2% | 1 em 82.8 |
| AKs (qualquer mão suited específica) | 4 | 0.3% | 1 em 331.5 |
| AKo (qualquer mão off-suit específica) | 12 | 0.9% | 1 em 110.5 |
| AA (qualquer par de mão) | 6 | 0.5% | 1 em 221 |
| KK+ | 12 | 0.9% | 1 em 110.5 |
| QQ+ | 18 | 1.4% | 1 em 73.7 |
| JJ+ | 24 | 1.8% | 1 em 55.3 |
| TT+ | 30 | 2.3% | 1 em 44.2 |
| QQ+, AK | 34 | 2.5% | 1 em 39 |
| JJ+, AK | 40 | 3.0% | 1 em 33.2 |
| TT+, AK | 46 | 3.4% | 1 em 28.8 |
| Quaisquer cartas suited, sem par | 312 | 23.5% | 1 em 4.3 |
| Quaisquer cartas off-suit, sem par | 936 | 70.6% | 1 em 1.4 |
| Qualquer par de mão | 78 | 5.8% | 1 em 17 |
| Quaisquer suited connectors | 52 |
3.9% | 1 em 25.5 |
Probabilidades de Completar uma Mão no Flop
O capítulo anterior abrangia a probabilidade de receber certas combinações de hole cards pré-flop. Mas e que tal falarmos de qual a probabilidade dessas hole cards melhorarem (e até que ponto) em flops específicos?
Segue uma tabela de várias probabilidades para ler e reler até se sentir preparado a lembrar-se delas quando estiver nas mesas:
| As Suas Hole Cards | Flop (A Sua Mão) | Probabilidade (%) | Odds |
|---|---|---|---|
| Cartas sem par | Um Par | 29.0% | 1 em 3.5 |
| Par de Mão | Um Set | 11.8% | 1 em 8.5 |
|
Cartas Conectadas (JT até 54) |
Um Straight | 1.3% | 1 em 77 |
| Suited Connectors | Um Flush | 0.8% | 1 em 119 |
Melhorar os Seus Draws
Um out no poker é uma carta que o ajudará a melhorar a força da sua mão. Os outs mais frequentes são aqueles que ajudarão um jogador a completar um straight ou flush.
Segue uma tabela que explica as odds de melhorar a sua mão, dependendo do número de outs que tem:
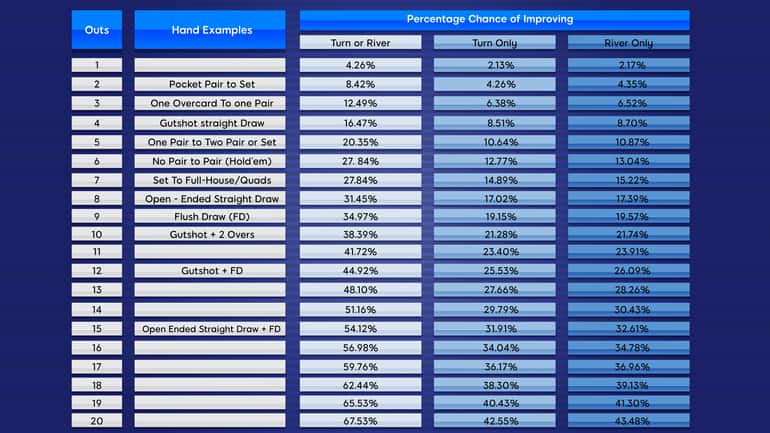
O Que São Pot Odds no Poker?
As pot odds (em português, probabilidades do pote) no poker levam em consideração o número de “outs” que possui (cartas que podem melhorar a sua mão), relacionando-as com o montante em dinheiro que tem de colocar (call) para ver outra carta.
Este cálculo é usado para determinar se o call para "perseguir" o seu draw é uma jogada lucrativa a longo prazo. Assim, quando os jogadores fazem a pergunta: “As pot odds são importantes?” - a resposta é um grande e bem demonstrativo SIM!
Lembre-se que o poker é um jogo que lida mais com vencer a longo prazo do que com sessões curtas e individualizadas. Utilizando as seguintes informações sobre as pot odds, poderá depois tomar muitas decisões + EV nas mesas.
Como Ler as Pot Odds em Percentagens, Frações e Rácios
Se tem 33% de possibilidade de melhorar a sua mão, essa percentagem pode ser expressa como "1/3". A cada três vezes que fizer call para tentar melhorar, completará a sua mão num desses momentos (em média).
Contudo, é preciso converter essas frações em rácios para poder relacioná-las com as pot odds.
No poker, estas probabilidades são expressas no seguinte formato quando tenta melhorar a sua mão:
Número de vezes que não completará a sua mão
---------------------------------------------------------------------
Número de vezes que completará a sua mão
Um exemplo disto seria 2:1 (que seria lido como "2 para 1").
Também pode ser expresso como 33% (percentagem) = 1/3 (fração) = 2:1 (rácio).
Fórmula de Pot Odds no Poker
Agora que entendemos os rácios em relação às probabilidades de melhorar a nossa mão de poker, vamos aplicar o mesmo conceito para entender as pot odds.
Vamos supor que estão €50 no pote principal e alguém aposta €50 adicionais. Agora, há um total de €100 no pote e terá de pagar uma aposta de €50.
As pot odds neste cenário apresentam um rácio de €100 para €50, ou 2 para 1.
A fórmula para determinar isto é a seguinte:
€ existente no pote principal + € colocado no pote durante a ronda de apostas atual
----------------------------------------------------------------------------------------------------
€€€ que tem de pagar (call)
Para outro exemplo, vamos supor que já existem €200 no pote principal. Nesta ronda de apostas, o Jogador 1 aposta €100, o Jogador 2 paga €100, e agora é a sua vez de agir.
Quais são as suas pot odds?
Utilizando a fórmula acima, chegamos à seguinte equação: €400 : €100 ou 4 para 1
(€200 no pote principal) + (€200 desta ronda de apostas)
--------------------------------------------------------------------------
(€100 que tem de pagar (call))
Como Funcionam as Pot Odds

O próximo passo para determinar se temos, ou não, as pot odds corretas para fazer call, relaciona as pot odds que calculámos com as possibilidades de melhorarmos a nossa mão. (Vamos aprender exatamente como calcular as nossas probabilidades de melhorar no próximo capítulo).
Colocando as coisas de modo simples, se as nossas probabilidades de melhorar para uma mão vencedora forem maiores do que as pot odds que estamos a receber para o call, então o call torna-se a jogada certa e a mais lucrativa.
Vamos supor que estamos a jogar Texas Hold'em e temos 8-7 de naipes diferentes. A board é K-5-6-2 rainbow. Atualmente, o valor da nossa mão é extremamente fraco (8-alto), mas temos a possibilidade de fazer a melhor sequência possível (nut straight) se um 4 ou 9 virar no river.
Perante um baralho padrão de 52 cartas, já conhecemos 6 dessas cartas ao turn (2 na nossa mão e 4 na mesa). Portanto, das 46 cartas restantes no baralho que podem virar no river, apenas 8 delas melhorarão a nossa mão (4 quadras e 4 noves). Este cálculo pode ser expresso como uma fracção de 8/46.
Podemos então usar esse rácio para relacionar “cartas no river que não melhorarão a nossa mão” com “cartas no river que melhorarão, de facto, a nossa mão”:
- 8 cartas no river vão ajudar
- 46 cartas desconhecidas - 8 cartas que nos ajudarão = 38 cartas que não nos ajudarão
- 38 cartas que não nos ajudarão: 8 cartas que nos ajudarão
- 38:8
- 4.75:1
O rácio de 4.75 para 1 indica que, por cada 4.75 vezes que não melhoramos, uma vez melhoramos. Assim, para fazermos um call lucrativo aqui, precisamos de ter pot odds superiores a 4.75 para 1 (ou seja, €500 já no pote perante uma aposta de €100).
Regras Básicas de Probabilidades no Poker
Obviamente, será difícil olhar para esta tabela de cada vez que quiser saber quais as probabilidades da sua mão melhorar e depois relacionar essa informação com as pot odds que está a receber. Por isso, para lhe dar um atalho básico, utilize o seguinte truque para o ajudar a calcular a probabilidade das suas mãos melhorarem:
Se multiplicar o número de outs que tem no flop por 4, terá uma ideia sólida da probabilidade de completar a sua mão no turn ou no river (com duas cartas por virar).
Se multiplicar o número de outs que tem no flop ou no turn por 2, ficará com uma aproximação da probabilidade de completar a sua mão na street imediatamente a seguir.
Por vezes, também pode querer variar o número de outs que o ajudarão, para considerar as probabilidades desses mesmos outs ajudarem o seu adversário a melhorar para uma mão melhor que a sua.
Por exemplo, se acha que o seu adversário pode ter um flush draw mais alto ou se a board dobrar dando-lhe um flush a si e talvez um full house ao seu adversário, você pode reduzir ligeiramente o número dos seus outs (ex.: 8.5 outs em vez de 9). Este ajuste considerará esta possibilidade quando relacionar o resultado com as pot odds e depois poderá prosseguir com a mão mais confiante das contas que fez.
Como Converter Pot Odds em Percentagens
Agora que aprendemos a calcular as pot odds e as probabilidades de melhorar, é hora de relacionar as duas para ver se temos as probabilidades certas para fazer o call.
No entanto, ao usar a “Regra de 2 e 4”, vai ficar com uma percentagem, enquanto que ao calcular as pot odds, fica com um rácio (como 2 para 1 ou 2:1)
Assim, é importante poder converter percentagens em rácios e vice-versa, se desejar determinar rapidamente se está a obter o valor certo, ou não, para o call.
Vamos começar por aprender como converter percentagens em rácios.
PERCENTAGENS PARA PROBABILIDADES:
Utilizando a “Regra de 2 e 4”, com 9 outs e 2 cartas por vir, temos cerca de 36% de probabilidades de melhorar a nossa mão para um flush. Através de um cálculo simples, podemos deduzir que, aproximadamente 64% das vezes, não completamos o nosso draw.
Ao converter percentagens em rácio, deve sempre colocá-las no seguinte formato:
(probabilidade de não melhorar a sua mão) : (probabilidade de melhorar a sua mão)
Usar este formato vai deixar-nos com um rácio de 64:36, ou cerca de 2 para 1 - um rácio que pode ser facilmente comparado às nossas pot odds. Quanto mais praticar este processo (pot odds vs percentagem), melhor será a sua capacidade de determinar as probabilidades de melhorar a sua mão.
PROBABILIDADES PARA PERCENTAGENS:
Vamos virar um pouco as coisas e ver como podemos transformar as pot odds em percentagens. Digamos que alguém faz uma aposta de ½ pote, o que nos daria 3 para 1 num call (alguém apostaria €50 num pote de €100. O pote é agora de €150 e você terá de pagar €50 se quiser fazer call, obtendo pot odds de 3 para 1).
Ao transformar este rácio numa fracção, podemos calcular facilmente a percentagem, como vamos ver mais abaixo:
(preço que precisa pagar / preço que precisa pagar + dinheiro já no pote)
Neste exemplo, o preço que devemos pagar é €50. Portanto, o (preço que temos que pagar(call)) + (o dinheiro que já está no pote) seria €50 + €150, dando-nos uma fração de €50/€200.
50/200 = 0,25 que pode ser facilmente convertido numa percentagem de 25% ao multiplicar 0,25 por 100.
Esta percentagem, em relação à força da sua mão, significa que precisaria de ter mais de 25% de possibilidade de ganhar a mão para efetuar um call lucrativo.
Se tal ainda lhe parece difícil, não se preocupe! Quanto mais praticar o cálculo de probabilidades, melhor ficará.
Mais ainda, para o ajudar, replicámos a tabela de cima e adicionámos odds em rácio já calculadas para si!
| 1 Carta por Vir |
2 Cartas por Vir |
||||||
|---|---|---|---|---|---|---|---|
| FLOP p/ TURN | TURN p/ RIVER |
TURN e RIVER |
|||||
| OUTS | EXEMPLOS MÃOS | % | ODDS | % | ODDS | % | ODDS |
| 1 | 2.13% | 45.95 : 1 | 2.17% | 45.08 : 1 | 4.26% | 22.50 : 1 | |
| 2 | Pocket Pair para Set | 4.26% | 22.47 : 1 | 4.35% | 21.99 : 1 | 8.42% | 10.88 : 1 |
| 3 | 1 Overcard para 1 Par | 6.38% | 14.67 : 1 | 6.52% | 14.34 : 1 | 12.49% | 7.01 : 1 |
| 4 | Gutshot Straight Draw | 8.51% | 10.75 : 1 | 8.70% | 10.49 : 1 | 16.47% | 5.07 : 1 |
| 5 | 1 Par para 2 Pares ou Set | 10.64% | 8.40 : 1 | 10.87% | 8.20 : 1 | 20.35% | 3.91 : 1 |
| 6 | Sem Par para Par (Hold'em) | 12.77% | 6.83 : 1 | 13.04% | 6.67 : 1 | 24.14% | 3.14 : 1 |
| 7 | Set para Full-House / Quads | 14.89% | 5.72 : 1 | 15.22% | 5.57 : 1 | 27.84% | 2.59 : 1 |
| 8 | Open-Ended Straight Draw | 17.02% | 4.88 : 1 | 17.39% | 4.75 : 1 | 31.45% | 2.18 : 1 |
| 9 | Flush Draw | 19.15% | 4.22 : 1 | 19.57% | 4.11 : 1 | 34.97% | 1.86 : 1 |
| 10 | Gutshot + 2 Overcards | 21.28% | 3.70 : 1 | 21.74% | 3.60 : 1 | 38.39% | 1.60 : 1 |
| 11 | 23.40% | 3.27 : 1 | 23.91% | 3.18 : 1 | 41.72% | 1.40 : 1 | |
| 12 | Gutshot + Flush Draw | 25.53% | 2.92 : 1 | 26.09% | 2.83 : 1 | 44.96% | 1.22 : 1 |
| 13 | 27.66% | 2.62 : 1 | 28.26% | 2.54 : 1 | 48.10% | 1.08 : 1 | |
| 14 | 29.79% | 2.36 : 1 | 30.43% | 2.29 : 1 | 51.16% | 0.95 : 1 | |
| 15 | Open-Ended Straight Draw + FD | 31.91% | 2.13 : 1 | 32.61% | 2.07 : 1 | 54.12% | 0.85 : 1 |
| 16 | 34.04% | 1.94 : 1 | 34.78% | 1.88 : 1 | 56.98% | 0.76 : 1 | |
| 17 | 36.17% | 1.76 :1 | 36.96% | 1.71 : 1 | 59.76% | 0.67 : 1 | |
| 18 | 38.30% | 1.61 : 1 | 39.13% | 1.56 : 1 | 62.44% | 0.60 : 1 | |
| 19 | 40.43% | 1.47 : 1 | 41.30% | 1.42 : 1 | 65.03% | 0.54 : 1 | |
| 20 | 42.55% | 1.35 : 1 | 43.48% | 1.30 : 1 | 67.53% | 0.48 : 1 |
A partir daqui, poderá relacionar as suas probabilidades com as pot odds e, com relativa facilidade, determinar se deve, ou não, fazer call.
Quando Fazer Call Utilizando Pot Odds

Se pudermos determinar o número de outs que temos para melhorar a nossa mão, ao usar o gráfico acima, podemos ver facilmente as probabilidades em qualquer situação.
A partir daí, simplesmente comparamos essas probabilidades com as pot odds. Se as suas probabilidades de melhorar são melhores que as pot odds, então tem as pot odds corretas para o call.
Para simplificar ainda mais, ao comparar os números no seu rácio, se o número à esquerda do rácio das suas pot odds for maior que o da esquerda no seu rácio de PROBABILIDADES DE MELHORAR - então deve avançar para o call!
Para ilustrar este ponto, vamos usar este breve exemplo
EXEMPLO DE MÃO:
Tem 6 outs e apenas a carta do river para vir. Há €500 no pote principal e está a apostar €100.
Tem as pot odds certas para o call?
Em primeiro lugar, é necessário calcular as nossas probabilidades de melhorar a nossa mão.
Na tabela de poker acima, podemos ver que essas probabilidades são de 6,67 para 1 (quando houver 6 outs).
Em segundo lugar, temos que determinar as nossas pot odds. Pegue nos €500 do pote principal e adicione-os à aposta de €100 dos seus adversários. Isso dá €600 que poderia ganhar com um call à aposta de €100.
Portanto, as suas pot odds são de 6 para 1.
- Pot Odds: 6 : 1
- Probabilidades de melhorar: 6.67 para 1
Como o número à esquerda (exibido a negrito) para as pot odds NÃO é maior que as nossas probabilidades de melhorar (6–6,67), NÃO temos claras pot odds suficientes para o call.
No entanto, só porque não tem as pot odds corretas para o call, tal não significa que deva sempre desistir da sua mão ao enfrentar essa aposta. Da mesma forma, quando tem as pot odds corretas, tal não significa que deve sempre optar pelo call.
Existem outras considerações que deve ter em conta antes de desistir da sua mão.
Vamos aprofundar um pouco mais sobre algumas delas.
Notas Adicionais
- Call no Flop: Lembre-se que se pagar no flop e não completar o seu draw no turn, poderá ainda enfrentar outra aposta no turn. Esse cenário pode afetar a maneira como usa a "Regra de 2 e 4" nos seus cálculos, pois também não veria a carta de borla no river.
- Outros jogadores atrás de si: Os outros jogadores que ainda irão agir, também podem fazer call, ou potencialmente até fazer raise! Se acha que eles podem pagar (call), pode levar isso em consideração ao determinar as suas pot odds. Se acha que eles podem fazer raise, um fold pode mesmo ser a melhor jogada.
- Fold Equity: As pot odds referem-se geralmente ao facto de fazer call, ou não, com um draw ser uma jogada lucrativa. No entanto, deve sempre equilibrar o seu range de mãos e considerar outras possibilidades também - uma delas sendo fazer raise quando lhe parece uma boa solução. Esta jogada é considerada um "semi-bluff", onde pode ganhar ao (1) melhorar a sua mão numa ronda posterior; ou (2) fazer o seu adversário desistir imediatamente.
- Probabilidades implícitas: as probabilidades implícitas referem-se a quanto dinheiro pode ser ganho em rondas futuras de apostas se realmente completar o seu draw. Por exemplo, muitas vezes, as pessoas com um straight ou flush draw no flop não têm as pot odds expressas corretas para pagar uma aposta com lucro, para ver se completarão o draw no turn ou no river. Contudo, se eles concluírem o draw, geralmente colocam as esperanças em ganhar outra ou duas apostas nas rondas futuras para compensar a diferença no call sem primeiro terem as probabilidades adequadas e bem expressas.
- Equity vs. Range do Vilão: Pot Odds vs. Equity - este é um conceito que nem todos os jogadores de poker conseguem diferenciar. Embora o termo “pot odds” se refira obter, ou não, o preço certo para fazer call, a equity/equidade refere-se a quanto dinheiro do pote deve ser seu com base na percentagem de vezes que a sua mão ganhará contra a mão ou range de mãos de um vilão.
Como Calcular Pot Odds em Texas Hold'em
Ao longo deste artigo, mostrámos imensas informações sobre as pot odds - quais são, os diferentes tipos existentes, como calculá-las, como calcular as suas possibilidades de melhorar e como relacionar esses dois elementos.
É agora altura de colocar tudo o que aprendeu em alguns exemplos, especificamente para o Texas Hold'em.
Usar as pot odds no Texas Hold'em vai certamente ajudá-lo a vencer nas mesas. Embora o No Limit Hold'em possa usar princípios de probabilidades implícitas (como pode ganhar muito mais ao escolher livremente exatamente quanto deseja apostar ou aumentar num determinado momento), o Limit Hold'em usa o conceito de pot odds expressas incrivelmente bem!
Vamos debruçar-nos sobre dois exemplos diferentes de No Limit vs. Limit, lidando especificamente com as pot odds para um flush.
EXEMPLOS DE MÃO: Pot Odds de Call com Flush Draw
Recebeu K♥Q♥. Joga-se o turn da board A-8-2-J com 2 copas. Estão €60 no pote. Você e o seu adversário têm €200 para trás e o seu adversário aposta €20.
Você tem as probabilidades expressas certas para o call? E as probabilidades implícitas (implied odds)?
Quanto dinheiro adicional precisaria ganhar no river para jogar esta mão de modo lucrativo?
- LIMIT HOLD’EM
NOTA: No Limit Hold'em, e porque haverá muitos jogadores a jogar cada mão e a fazer call em pequenas apostas durante o percurso, os potes podem ficar consideravelmente grandes em relação às apostas e aos limites de apostas à medida que as rondas de apostas progridem. Essa situação pode dar aos jogadores probabilidades corretas para perseguir os seus draws, sem precisar de ganhar dinheiro adicional nas rondas futuras através das probabilidades implícitas.
Utilizando as informações acima no cenário criado, vamos primeiro calcular todas as probabilidades. Temos um nut flush draw e um straight straw. 9 cartas iriam nos garantir um flush. Qualquer um dos quatro 10 nos daria uma sequência. No entanto, como não podemos contar o 10♥ duas vezes, isso dá-nos 12 outs para melhorar a nossa mão com uma carta por vir.
Multiplicamos os nossos outs por 2 para ficar a conhecer a nossa percentagem aproximada de vitórias na mão. Isso dá-nos 24% para melhorar para aquela que será, provavelmente, a mão vencedora (ou cerca de 3 para 1). Como agora existem €80 no pote após a aposta de €20 do vilão, precisamos pagar €20 para ganhar €80, dando exatamente 4:1 de probabilidades expressas num call. Perante este cenário, temos exatamente as probabilidades expressas corretas para o call.
Por outras palavras, mesmo se nunca ganharmos uma aposta extra no river, desde o momento em que pagamos e melhoramos, pagar esta aposta de €20 ainda assim seria uma jogada lucrativa. Esperamos ganhar uma média de €6,67 por cada vez que pagarmos (mais quaisquer lucros que possamos extrair ainda mais no river através das probabilidades implícitas)!
- NO-LIMIT HOLD’EM
Façamos uma pequena alteração no cenário descrito acima. Em vez de haver €60 no pote, digamos que estão apenas €20 quando o nosso adversário fizer a aposta de €20. Agora, teríamos hipóteses de 2 para 1 numa aposta (numa mão em que temos probabilidades de 3 para 1).
Perante este novo cenário, não podemos pagar (call) com base em probabilidades expressas, mas podemos pagar com lucro com base em probabilidades implícitas, se acharmos que podemos obter uma certa quantia de dinheiro do nosso adversário no river nos momentos em que o draw surgir.
Ter uma mão com probabilidades expressas que nos dão 3:1 (onde ganhamos cerca de 25% das vezes) significa que teremos que pagar a aposta de €20 agora para potencialmente ganhar 3 x €20 se o nosso draw se completar no river.
Assim, se finalmente conseguirmos ganhar pelo menos €60 no total, com o call à aposta no turn, tal tornar-se-á uma aposta break even (ou até lucrativa). Com €40 no pote antes de pagarmos, só precisamos de ganhar €20 adicionais do nosso adversário no river. Se completarmos o nosso draw e depois apostarmos €20, provavelmente será difícil para o nosso adversário desistir, obtendo tão boas pot odds no river.
O pote seria de €60 (excluindo a nossa aposta de €20), o que significa que eles teriam que pagar €20 para ganhar €80. Por outras palavras, eles teriam probabilidades de 4:1 e precisariam de ter apenas a melhor mão 20% das vezes para que esse call no river fosse lucrativo. Esse factor torna provável que eles façam call à nossa aposta por este preço tão bom.
Provavelmente, poderíamos extrair muito mais ao nosso adversário no river (até €30 ou €45 num pote de €60), tornando o call no turn muito lucrativo, com base nas probabilidades implícitas.
Como Calcular Pot Odds em Omaha
Calcular as pot odds em Omaha poker é muito semelhante ao Texas Hold'em.
A maior diferença, no entanto, diz respeito aos outs:
- Vai, muitas vezes, ter muito mais outs para melhorar a sua mão (provenientes das várias combinações de mãos de duas cartas com as suas duas cartas extra). De facto, não é incomum ter mais de 20 outs que podem melhorar a sua mão (mesmo com duas cartas por vir) com todos os "desenvolvimentos" possíveis em Omaha.
- Terá de ter mais cuidado com os outs negativos que possam melhorar mais a mão dos seus adversários do que a sua!
- Devido ao aumento do número de combinações de cartas individuais (e às probabilidades das pessoas chegarem ao showdown com mãos de poker muito melhores do que as normalmente encontradas no Hold'em), convém chegar o mais rapidamente possível à carta desejada.
EXEMPLO DE MÃO:
Tem A♥-T♥-9♣-8♦. O flop vem 7♥-6♥-2♣. o seu adversário aposta €100 num pote de €100. Cada um de vocês tem cerca de €1.000 para trás. O que deveria fazer? Tem as probabilidades expressas/implícitas corretas para fazer call?
Esta mão é muito forte! Embora atualmente você só tenha Ás alto, há uma quantidade incrível de cartas (outs) que podem ajudá-lo a melhorar:
- 4 Cincos para o nut straight;
- 3 Oitos para o nut straight;
- 3 Noves para o nut straight;
- 3 Dez para o nut straight;
- 5 cartas adicionais (excluindo as acima) que podem dar-lhe um nut flush.
Tem um total de 18 outs para melhorar a sua mão! Se é um jogador que normalmente está habituado a jogar Hold'em, provavelmente achará este número incrível!
Observando a nossa tabela de probabilidades de poker, veremos que, com 18 outs e 2 cartas por vir, temos 62% de probabilidade de melhorar a nossa mão no river! Temos até 38% de chances de acertar um dos nossos draws só no turn!
A única coisa com a qual nos devemos preocupar é a possibilidade de um adversário ter um set e a possibilidade de evoluir (melhorar para um full house). No entanto, após o flop, mesmo contra muitas combinações de mãos, mesmo contendo sets, ainda temos cerca de 50% de probabilidades de ganhar esta mão (na pior das hipóteses)!
Com probabilidades incríveis de vencer aqui, as pot odds são quase irrelevantes (excepto num turn mais complicado). Em vez disso, o nosso foco deve estar em como podemos extrair mais dinheiro com a possibilidade de eliminar alguém!
Visto que temos 62% de probabilidades de ganhar, temos muito mais hipóteses do que as probabilidades de 2 para 1 que precisamos para o call. Talvez, em vez de simplesmente fazer o call aqui, para maximizar o nosso valor esperado com um draw tão forte, talvez tente aumentar!
No pior dos casos é que vamos consegui-lo contra um set (que, como mencionado, seria um 50/50).
Calcular Probabilidades no Poker Heads-Up

Algo muito importante que temos de sublinhar é a diferença de como a equity está dividida em situações em que estamos contra um adversário (heads-up) em comparação a situações em que estamos contra vários.
Contra vários jogadores, a equity da mão de cada um será mais baixa do que numa situação de heads-up porque a mesma estará dividida e espalhada por todos os jogadores ainda na disputa do pote.
Utilizemos par de Ases como exemplo. Contra o seguinte range do(s) seu(s) oponente(s):
- Qualquer par de mão;
- Qualquer Ás suited;
- Quaisquer duas cartas Broadway;
- Suited connectors: 54s até T9s
- One gapped suited connectors: 96s até J9s
- Q9s, K9s.
Segue a percentagem de equity que par de Ases tem nesta situação contra:
- Um adversário: 83.4%
- Dois adversários: 70.6%
- Três adversários: 60.2%
- Quatro adversários: 51.4%
Como vê, quantos mais adversários estiverem na mão, menor é a probabilidade de Ases ganharem. E é por isso que é tão vantajoso jogar estes grandes pares de mão heads-up, em potes com um SPR baixo.
E em situações em que tem draws num cenário contra vários jogadores, ter mais adversários não muda o número de outs que tem para melhorar. Contudo, as probabilidades de alguém ter um draw melhor que o seu ou uma mão que, mais tarde, poderá sobrepor-se à sua, certamente aumentarão.
Adicionalmente, quando a ação é multiway, é essencial sublinhar que os jogadores têm tendência a fazer menos bluffs e apostar por valor mais frequentemente (quando apostam).
Portanto, considerando os últimos dois pontos, é crucial lembrar-se sempre de contabilizar quantos adversários estão numa mão e determinar a melhor forma de jogar com base nisso.
Sumário: Porquê Calcular Pot Odds
Para aumentar a probabilidade de ganhar no poker, deve habituar-se a calcular pot odds e probabilidades que lhe são apresentadas no decorrer das mãos. Familiarize-se com outs e cálculo de percentagens de forma a ser capaz de relacionar rapidamente estes aspetos com as pot odds que está a receber. Depois, será muito mais simples saber se pode fazer call lucrativamente.
(Para mais informação sobre as pot odds e o tamanho das apostas, leia o nosso artigo dedicado ao Bet Sizing.)
Lembre-se, também, de que não precisa de fazer sempre "apenas call" quando tem um draw. Por vezes, pode ser vantajoso apostar ou fazer raise. Dessa forma, poderá ganhar de duas formas: ou porque a sua mão efetivamente melhora numa street futura ou porque consegue fazer com que o seu adversário faça fold.
Às vezes, quando jogar, pode não ter as melhores pot odds para fazer call (ou seja, probabilidades expressas), mas em determinadas situações, há potencial para compensar nas próximas rondas de apostas através das probabilidades implícitas. Outras vezes, vai desistir de muitos dos seus draws fracos simplesmente porque não tem muita equity na mão.
Por fim, lembre-se sempre de que o poker é um jogo de habilidade que pode ser melhorada ao longo do tempo. Quanto mais tentar usar as habilidades de poker que aprendeu aqui, lidando com probabilidades e outs, mais terá uma "intuição" de como elas funcionam e como usá-las corretamente no seu jogo.
De facto, provavelmente antes que se aperceba, tudo se tornará como um sexto sentido para si!
Tudo de bom ao usar estas novas informações e boa sorte nas mesas!
Primeira Publicação a 31 de Outubro de 2019


